8 Tips and Tricks for Using Python as a Calculator App

You may have heard that you can use Python’s interactive mode as a calculator. There are plenty of functions that let you turn Python into a scientific or even a graphing calculator.

8

Calculate Exponents, Roots, and Logarithms

Exponents, roots, and logarithms are common math operations are some of the functions you can use in Python to replace a handheld scientific calculator.

To raise a base to the nth power, just use the ** operator. For example, to square the number 2:

        
2**2
    

Many other languages like Excel use the ^ (caret) operator for exponents, so that might trip you up if you’re used to them. If you get an error message, make sure you used the right operator.

Square roots are also simple. You can use the math library in Python. There’s a function called sqrt that takes the square root of a number:

        
import math
math.sqrt(81)
    

This will return the number 9. For numbers that aren’t perfect squares, it will return a decimal approximation the way a handheld scientific calculator would. The cbrt function works the same way, but with cube roots.

To take a root higher than 3, raise it to the 1/n power using the exponent operator. For example, to take the eighth root of 256:

        
256**(1/8)
    

The parentheses are there to tell Python we’re raising the number to a fractional exponent. Otherwise, it will raise 256 to the first power, giving 256, then divide that by 8, which is not what we want. With the parenthesis, it will return 8, because 2 to the eighth power is 256.

This brings us to logarithms, which are backward exponents. The log function takes the logarithm of a number using a certain base. By default, it uses the natural logarithm with the constant e (2.17828…) as a base:

        
math.log(42)
    

To use the common logarithm, supply the base as the second argument:

        
math.log(42,10)
    

The math library developers have created a shortcut for the common logarithm, since it’s, to pardon the pun, common. Use the log10 function:

        
math.log10(42)
    

Logarithms to base 2 are also common in computing, and there’s a similar function with 2 as the base. To find out how many bits are needed for a number, use the log2 function:

        
math.log2(512)
    

You can use a different base by taking the natural or common logarithm of a number and dividing it by the logarithm of the base you want to use. For example, to take the logarithm of 81 to the base 3:

        
math.log(81) / math.log(3)
    

This will return 4, because 3 to the 4th power is 81. You can check it by taking the antilogarithm of base 3:

        
3**4
    

7

Use Constants

Speaking of mathematical constants, you can also use the constants of e and pi easily with the math library.

You might remember that the area of a circle is pi multiplied by the square of the radius. Here’s how to calculate the area of a circle with a radius of 6 units:

        
import math
math.pi * 6**2
    

6

Use Trigonometric Functions

If you use trigonometric functions on a scientific calculator, the math library lets you use them in Python. Sine, cosine, and tangent as well as the corresponding inverse trig functions are available.

These functions operate on radians, but you can convert them into radians with the degrees function. To convert 60 degrees into radians:

        
import math
math.radians(60)
    

To take the sine of this angle, use the sin function.

        
angle = math.radians(60)
math.sin(angle)
    

We can get our original angle back by using asin, the inverse sine or arcsine:

        
math.asin(1.0471975511965976)
    

We can also use the “_” underscore operator in interactive mode to get the previous result to save typing.

        
math.asin(_)
    

There’s also a function to convert radians to degrees:

        
math.degrees(_)
    

This will bring us back to our original measurement. The cos and acos and tan and atan functions work the same way.

5

Solve Equations With SymPy and NumPy

Python can do numerical calculations, but it can also solve algebraic equations with the right libraries. You don’t need expensive proprietary computer algebra systems like Mathematica or Maple. You can breeze through math and science problems with Python.

Let’s use SymPy to solve a simple equation, 3x + 5 = 7. This would be easy to do by hand but this will show what SymPy can do.

First, import SymPy:

        from sympy import *
    

Before we use x, we’ll have to define it as symbolic variable:

        
x = symbols('x')
    

We’ll use SymPy’s Eq function, as SymPy expects equations equal to 0.

        
eqn = Eq(3*x + 5,7)
    

Now we’ll use the solve function to solve for x:

        
solve(eqn,x)
    

The answer should be 2/3.

The isympy command-line app, will import SymPy into an interactive environment, define some common variables, including x, and set up pretty printing so that the results look more like they would in a textbook.

Let’s do something harder. A quadratic equation is more difficult to solve by hand. Fortunately, with SymPy you won’t have to remember the quadratic formula or how to complete the square. We’ll solve the quadratic equation x^2 + 4x +2 = 0. We can just go straight to solving it for x:

        
solve(x**2 + 4*x + 2,x)
    

The answers will be 2 minus the square root of 2 and 2 plus the square root of 2. Remember to explicitly define the multiplication, such as 4*x for 4x.

You can also solve a system of linear equations easily with NumPy. We’ll solve the first example equation from the Wikipedia page on systems of linear equations:

3x + 2y – z = 1

2x -2y + 4z = -2

-x + 1/2y – z = 0

We’ll use a matrix and vector to solve this. We don’t need to care about the variables. We just want the coefficients. We’ll use a 2-D array, or an array of arrays, to represent a coefficient matrix:

        
import numpy as np
A = np.array([[3,2,-1],[2,-2,4],[-1,1/2,-1]])
    

And we’ll use another array for the column vector of constants on the right-hand side of the system:

         b = np.array([1,-2,0])
    

And then wel’ll use NumPy’s linalg.solve function to solve it if the system has any solutions (not all systems of linear equations do)

        np.linalg.solve(A,b)
    

You’ll get back a list of solutions to the system, in this case 1, -2, and -2. These correspond to the variables of x,y, and z.

Many scientific calculators and spreadsheets like Excel have some statistical operations in them. You can do some simple statistics with the Statistics library.

Let’s create an array of a few numbers to serve as our data set

        data = [25,42,35]
    

To calculate the mean of a few numbers, put them in an array and use the mean function:

        
statistics.mean(data)
    

For the median:

        
statistics.median(data)
    

And the mode, the most frequently occurring value:

        
statistics.mode(data)
    

In this case, with each number appearing the same number of times, Python will print the first one.

3

Need Only One Function? Just Import It!

If you only need one or a few functions from a library for interactive use, you can import them.

If you just need the sine function from the math library, you can just import it like this:

from math import sin

Now you can use it without having to call the library first:

        
sin(42)
    

2

Calculate Factorials, Permutations, and Combinations

Basic combinatorial operations like factorial, permutations, and combinations are also available in Python. Once again, it’s the math library to the rescue:

        
from math import factoral, comb, perm
    

A factorial is a number times the next lowest number times the next lowest number all the way to 1. It’s abbreviated by the exclamation point. For example, 49 factorial is 49!

To calculate 49! use the factorial function from the math library we just imported:

        
factorial(49)
    

The result is a very big number. To compute how many combinations you can get by drawing 5 cards from a standard 52-card deck:

        
comb(52,5)
    

To calculate the permutations, that is, drawing cards where the order is important, use the perm function:

        
perm(52,5)
    

1

Plot a Function With SymPy

Sympy can not only solve equations, it can also plot them the way a graphing calculator would.

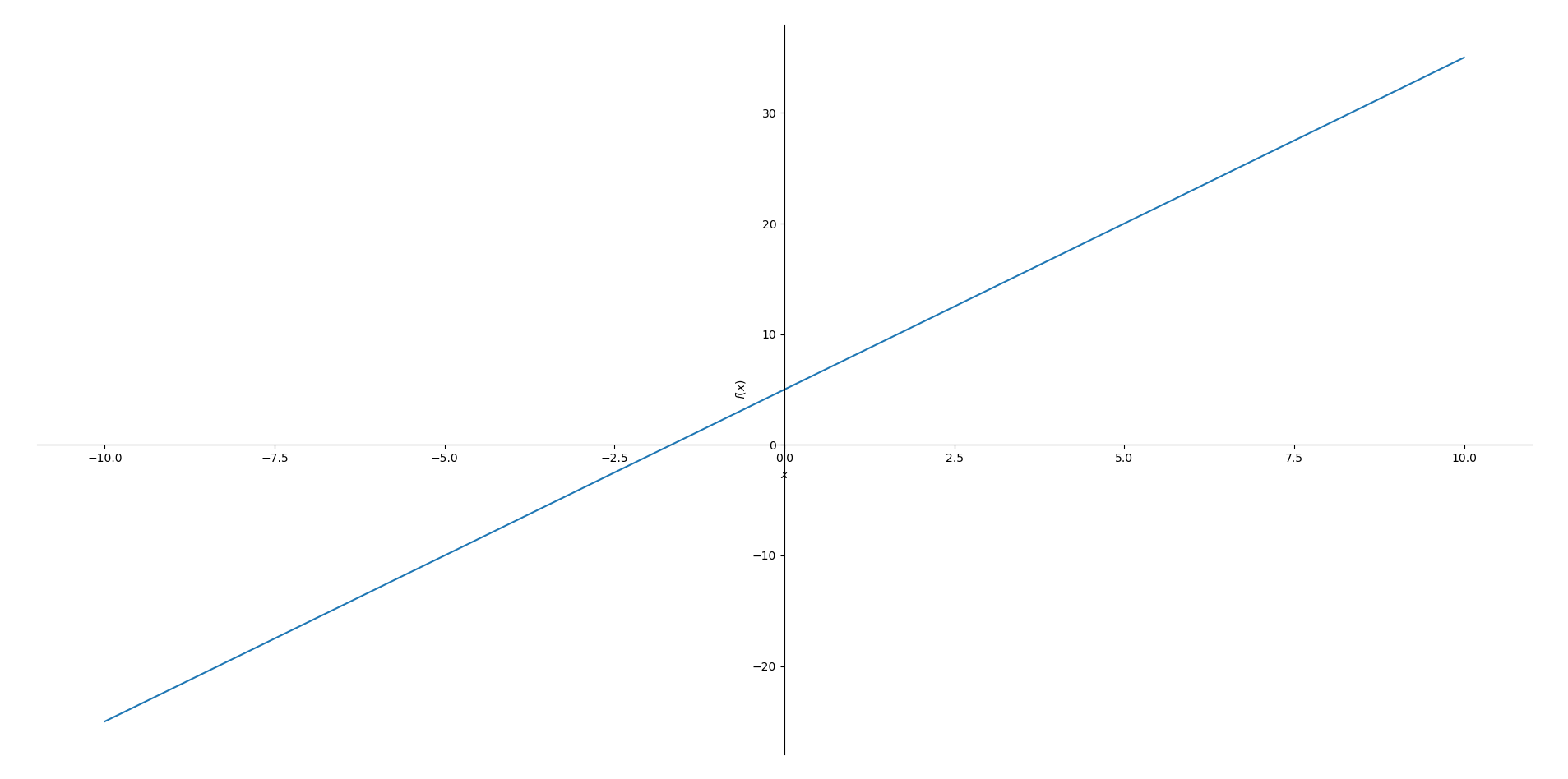
You can plot functions in the form y = mx+ b, where m is the slope and b is the intercept. We only need the mx + b part. For example, to plot y = 3x + 5

        
from sympy import symbols, plot
x = symbols('x')
plot(3*x + 5)
    

A window will pop up with the plot or it will appear in a Jupyter notebook. With all of these functions, you can keep that old scientific or graphing calculator in the drawer and use something that’s much cheaper and more flexible.